DAG（有向无环图）

what is DAG?

DAG（Directed acyclic graph）中文名称是有向无环图，简单来说，就是对于一个无回路的有向图。

如果一个有向图无法从任一个顶点出发经过若干条边回到该点，则这个图是一个有向无环图（DAG）。

有向无环图和树的关系：

因为有向图中一个点经过两种路线到达另一个点未必形成环，因此有向无环图未必能转化成树，但任何有向树均为有向无环图。

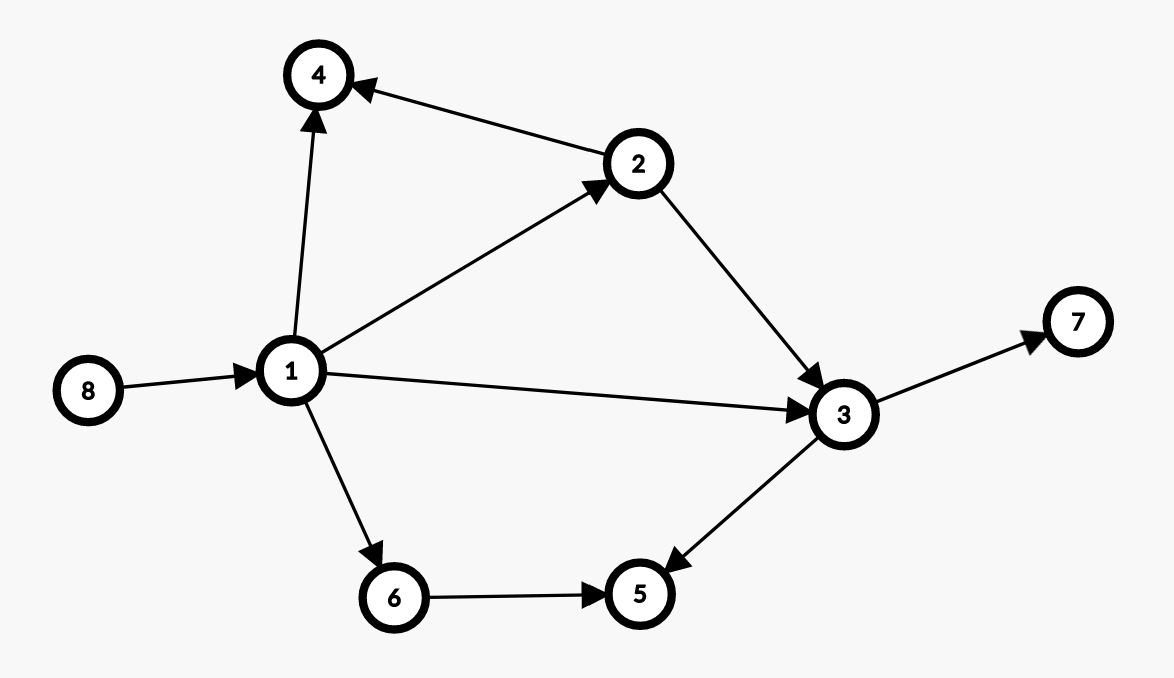
比如上图就是一个有向无环图，但是它不是树。

DAG 的性质与应用

性质

• 有向无环图一定存在拓扑序。
• 在一个有向无环图上，可以进行最长路的求解，具体做法为拓扑排序后进行 bfs。
• 在讲 kosaraju 时，我引用了一句话：“Every graph is the DAG of its strong connected conponents.”，译为“每个图都是关于其强连通分量的有向无环图”，那么，也就是说，我们按照强连通分量缩点，那么缩点后得到的新图一定是一个 DAG。

应用

• 有向无环图是描述含有公共子式的表达式的有效工具。
• 有向无环图是描述一项工程或系统的进行过程的有效工具。

Tarjan 算法与强连通分量

SCC 是什么？

关于 SCC 的前置知识，我在讲 kosaraju 的时候讲过了，还不会或者有兴趣的同学可以自己去看看😊。

强连通分量的定义：若两点能相互到达，则它们在一个强连通分量中。

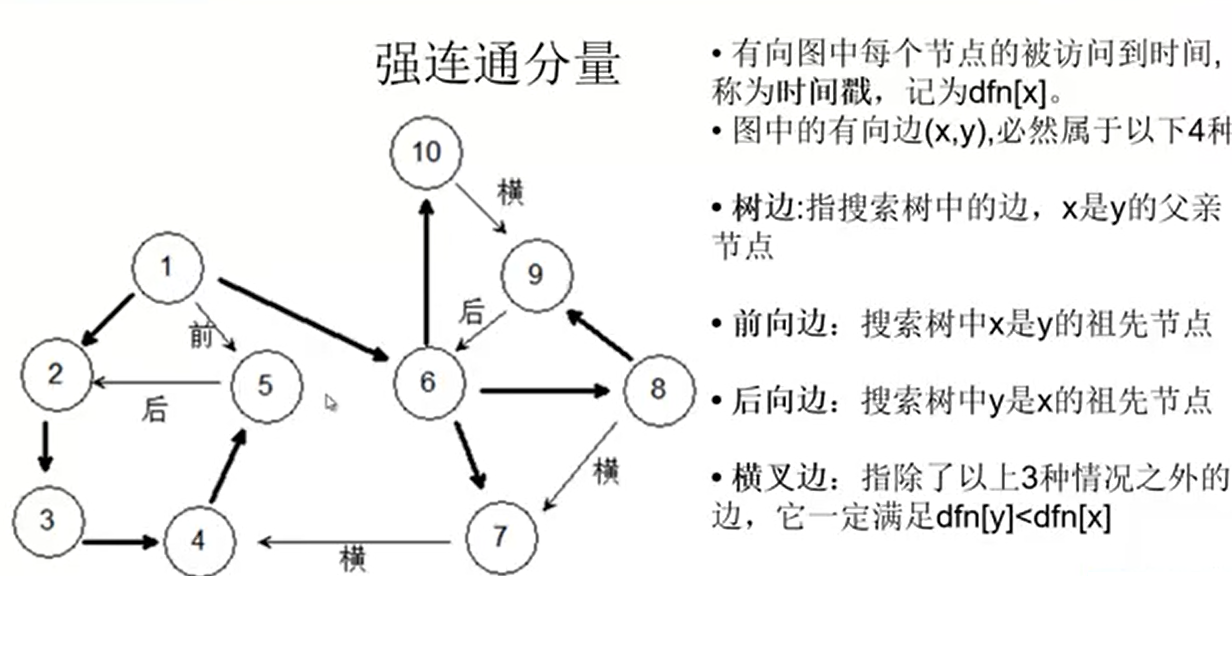
边的分类与有效性

横插、前向、后向边是什么？

树边：也就是搜索树上的边，是我们对整个图进行 dfs 时所调用的边。
横插边：我们将 dfs 的函数栈称之为 dfs 栈，在 dfs 时，如果现在搜到的点 $u$（在栈中）有一条边与一个不在 dfs 栈中的点 $v$ 相连，我们就成这条 $(u,v)$ 之间的边为横插边，比如 $(7,4)$ 这条边。
后向边：也可以叫做“返祖边”，即在 dfs 时，后被 dfs 到的点 $u$ 有一条非搜索树边与其 dfs 搜索树上他祖先的相连，比如 $(5,2)$ 这条边。
前向边：可以理解为反向的前向边，即在 dfs 时，后被 dfs 到的点 $u$ 有一条非搜索树边与其 dfs 搜索树上他祖先的相连，比如 $(1,5)$ 这条边。

那么，在运行 tarjan 算法的时候，我们有四种边可以选择，分别是树边、横插边、后向边、前向边，

哪一种边是有用的呢？

如果几个点在同一个强连通分量里，那么也就说明他们之间相互连通，搜索树上的边保证了从搜索树的根开始，经过简单的链，能够到达叶子节点，那么，若是强连通分量，我们需要保证能从叶子节点返回搜索树上其祖先才行，也就是说，我们需要一条边，从搜索树上深度大的点连向深度小的点，这种边显而易见的，就是返祖边（后向边）。

tarjan 算法是如何实现的？

先设定几个数组的意义，$dfn$ 数组表示每个结点的 dfs 序，$low$ 数组表示每个结点能够通过一条边到达的深度最小，且在搜索树上为其祖先的点（即通过返祖边能够到达的深度最小的祖先）。

tarjan 算法的实现过程一共有 $4$ 步：

• 假设现在正在搜索的节点为 $u$ 节点。

1. 对于 dfs 搜索的点，进行入栈操作，并且记录其在栈中，初始化节点 $u$ 的值 $low_u=dfn_u$。
2. 对于已经搜索过的节点，判断是否存在节点 $v$ 与 $u$ 之间有一条返祖边，判断的条件就是若点 $v$ 在 dfs 栈中，且点 $v$ 与点 $u$ 连同，则用 $dfn_v$ 更新 $low_u$，即 $low_u=\min(low_u,dfn_v)$。
3. 对于为访问过的且能连到的节点 $v$，进行扩展，继续搜索，搜索结束后，用 $low_v$ 更新 $low_u$，即 $low_u=\min(low_u,low_v)$。
4. 如果一个点的 $low_u=dfn_u$，说明对于这个点，无论如何，都不能通过返祖边连回搜索树上他的祖先了，他就是这个强连通分量里最深度最小的点，我们姑且称之为强连通分量头，那么一直执行出栈操作直到 $u$ 出栈为止，本次出栈的点就属于同一个强连通分量。

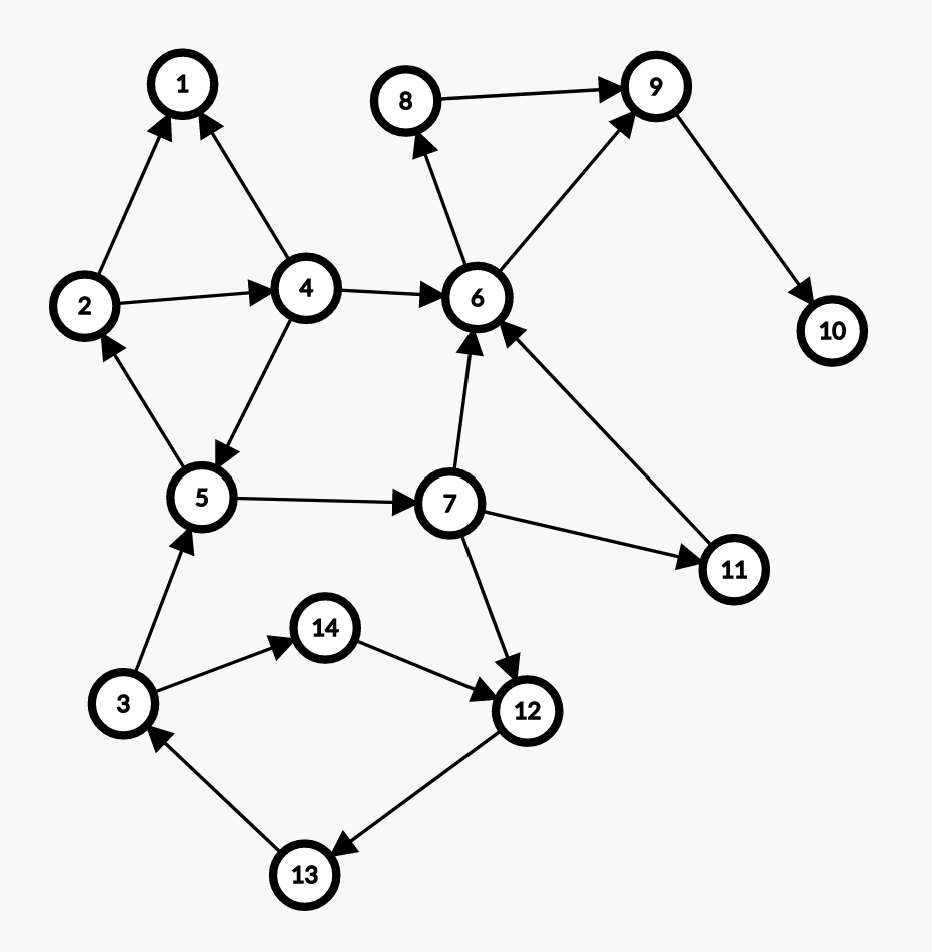
可以手动模拟一下上图，更好的理解代码，如不理解，请评论。