图与相关概念

1. 什么是图？

很简单，点用边连起来就叫做图，严格意义上讲，图是一种数据结构，定义为：$graph=(V,E)$，其中 $V$ 是一个非空有限集合，代表顶点（结点），$E$ 代表边的集合。

2. 图相关的定义和概念

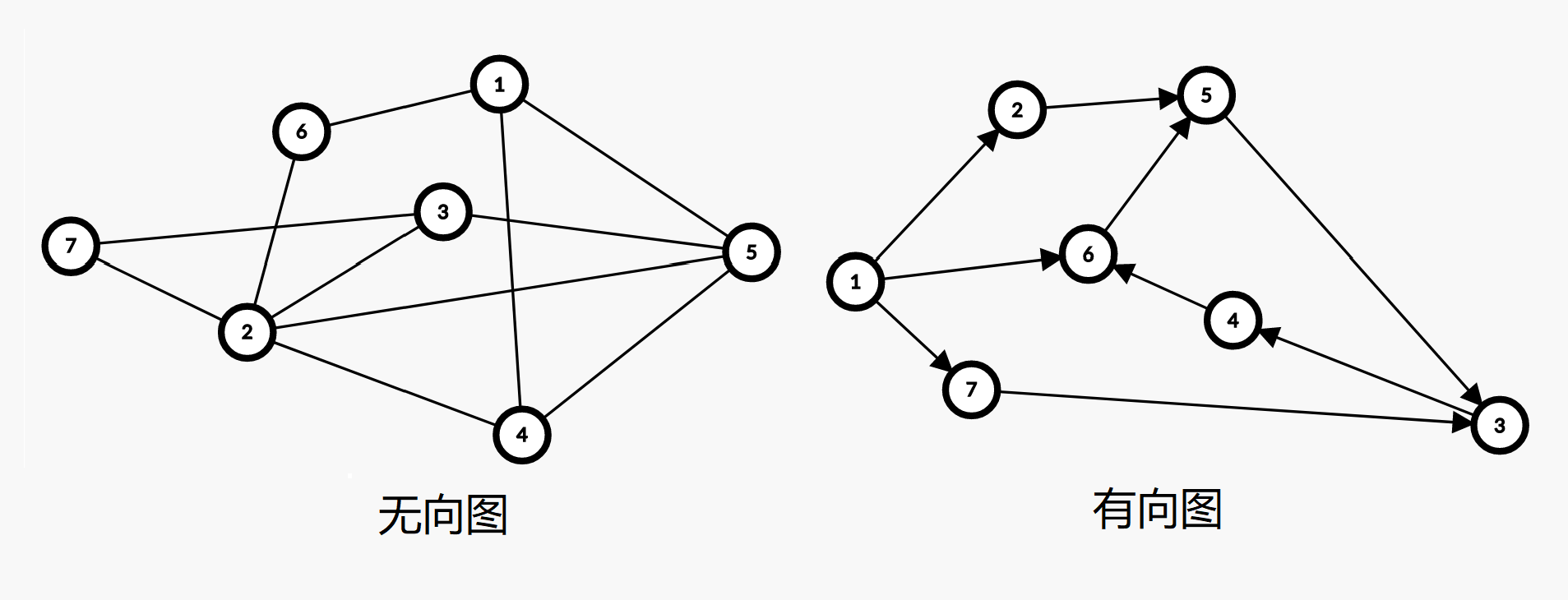
有向图：图的边有方向，只能按箭头方向从一点到另一点。(a)就是一个有向图。
无向图：图的边没有方向，可以双向。(b)就是一个无向图。

结点的度：无向图中与结点相连的边的数目，称为结点的度。
结点的入度：在有向图中，以这个结点为终点的有向边的数目。
结点的出度：在有向图中，以这个结点为起点的有向边的数目。
边权：边的“费用”，可以形象地理解为边的长度（顶点也可以有点权）。
连通：如果图中结点 $u$，$v$ 之间存在一条从 $u$ 通过若干条边、点到达 $v$ 的通路，则称 $u,v$ 是连通的。
回路：起点和终点相同的路径，称为回路，或“环”。
n 阶图：含有 $n$ 个点的图。
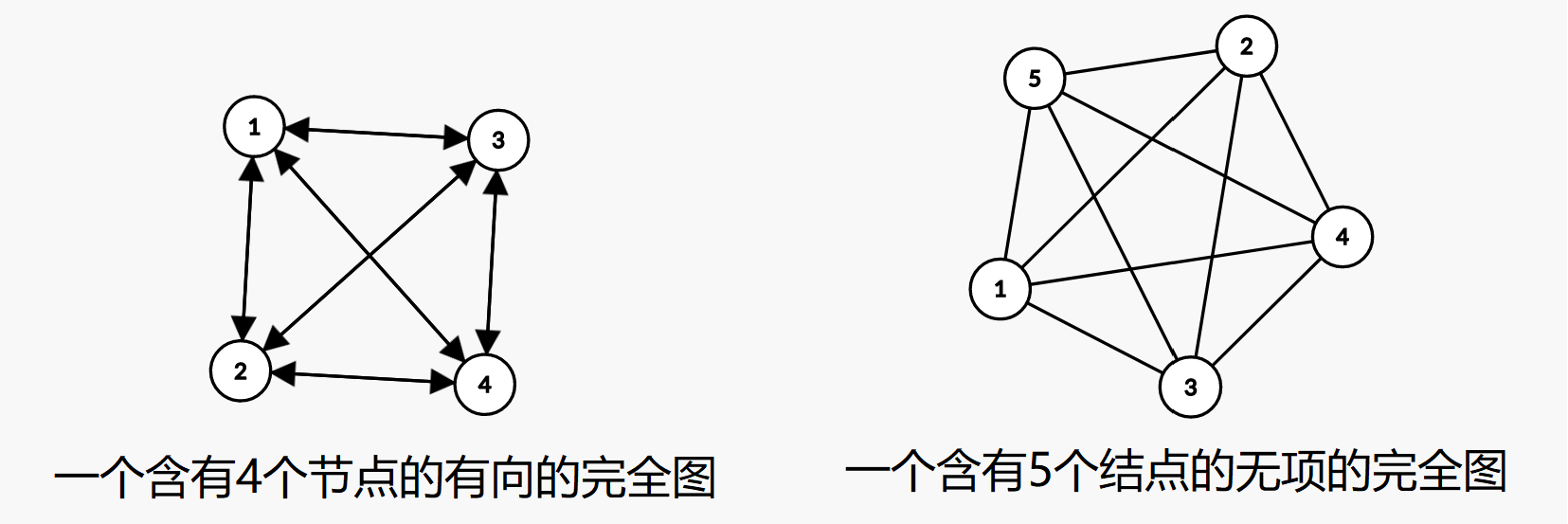
完全图：一个n 阶的完全无向图含有n*(n-1)/2 条边；一个n 阶的完全有向图含有n*(n-1)条边；

稠密图：一个边数接近完全图的图（没有明确判定条件）。
稀疏图：一个边数远远少于完全图的图（没有明确判定条件）。
强连通分量：有向图中任意两点都连通的最大子图。特殊地，单个点也算一个强连通分量，所以下图中有三个强连通分量：1-2-3，4-5-6-7 和 8。

重边：两个顶点中间有不止一条边。
自环：有一个节点到其本身的边。
简单图：没有重边和自环的图。
最短路：两节点之间的最短路径长度（带权图的路径最小边权和）。
源：入度为 $0$，出度不为 $0$ 的点。
汇：出度为 $0$，入度不为 $0$ 的点。