SCC 与 Tarjan 算法

Tarjan 算法与强连通分量

SCC 是什么？

关于 SCC 的前置知识，我在讲 kosaraju 的时候讲过了，还不会或者有兴趣的同学可以自己去看看😊。

强连通分量的定义：若两点能相互到达，则它们在一个强连通分量中。

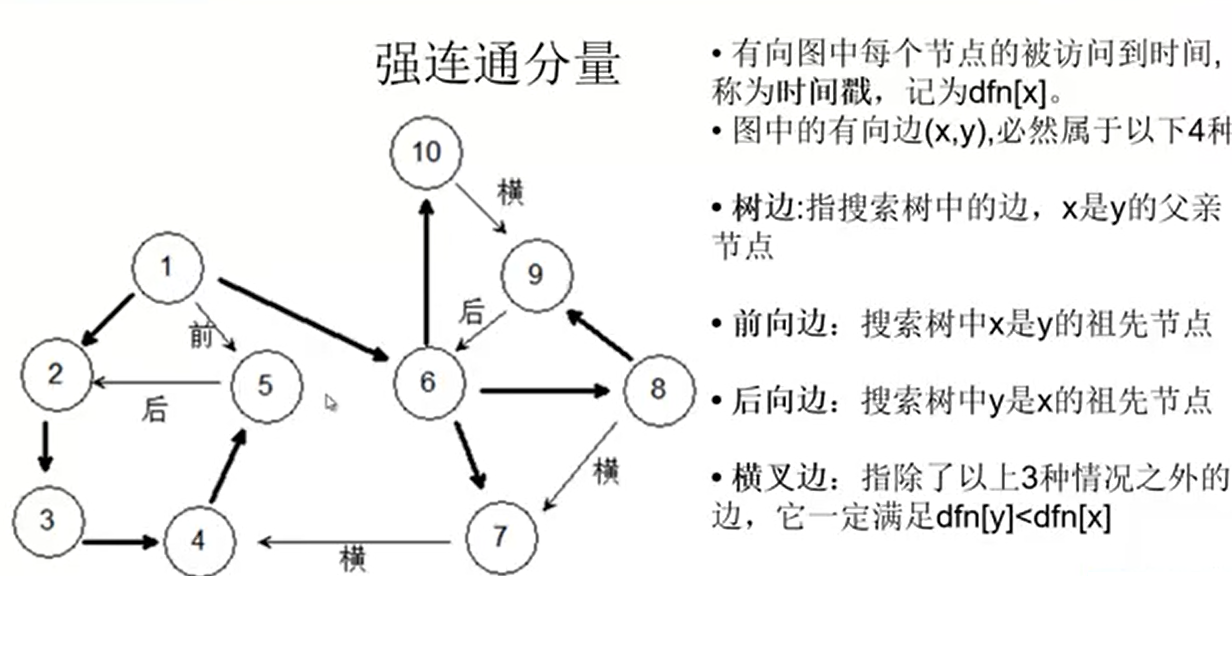
边的分类与有效性

横插、前向、后向边是什么？

树边：也就是搜索树上的边，是我们对整个图进行 dfs 时所调用的边。
横插边：我们将 dfs 的函数栈称之为 dfs 栈，在 dfs 时，如果现在搜到的点 $u$ （在栈中）有一条边与一个不在 dfs 栈中的点 $v$ 相连，我们就成这条 $(u,v)$ 之间的边为横插边，比如 $(7,4)$ 这条边。
后向边：也可以叫做“返祖边”，即在 dfs 时，后被 dfs 到的点 $u$ 有一条非搜索树边与其 dfs 搜索树上他祖先的相连，比如 $(5,2)$ 这条边。
前向边：可以理解为反向的前向边，即在 dfs 时，后被 dfs 到的点 $u$ 有一条非搜索树边与其 dfs 搜索树上他祖先的相连，比如 $(1,5)$ 这条边。

那么，在运行 tarjan 算法的时候，我们有四种边可以选择，分别是树边、横插边、后向边、前向边，

哪一种边是有用的呢？

如果几个点在同一个强连通分量里，那么也就说明他们之间相互连通，搜索树上的边保证了从搜索树的根开始，经过简单的链，能够到达叶子节点，那么，若是强连通分量，我们需要保证能从叶子节点返回搜索树上其祖先才行，也就是说，我们需要一条边，从搜索树上深度大的点连向深度小的点，这种边显而易见的，就是返祖边（后向边）。

tarjan 算法是如何实现的？

先设定几个数组的意义， $dfn$ 数组表示每个结点的 dfs 序， $low$ 数组表示每个结点能够通过一条边到达的深度最小，且在搜索树上为其祖先的点（即通过返祖边能够到达的深度最小的祖先）。

tarjan 算法的实现过程一共有 $4$ 步：

假设现在正在搜索的节点为 $u$ 节点。

对于 dfs 搜索的点，进行入栈操作，并且记录其在栈中，初始化节点 $u$ 的值 $low_u=dfn_u$ 。
对于已经搜索过的节点，判断是否存在节点 $v$ 与 $u$ 之间有一条返祖边，判断的条件就是若点 $v$ 在 dfs 栈中，且点 $v$ 与点 $u$ 连同，则用 $dfn_v$ 更新 $low_u$ ，即 $low_u=\min(low_u,dfn_v)$ 。
对于为访问过的且能连到的节点 $v$ ，进行扩展，继续搜索，搜索结束后，用 $low_v$ 更新 $low_u$ ，即 $low_u=\min(low_u,low_v)$ 。
如果一个点的 $low_u=dfn_u$ ，说明对于这个点，无论如何，都不能通过返祖边连回搜索树上他的祖先了，他就是这个强连通分量里最深度最小的点，我们姑且称之为强连通分量头，那么一直执行出栈操作直到 $u$ 出栈为止，本次出栈的点就属于同一个强连通分量。

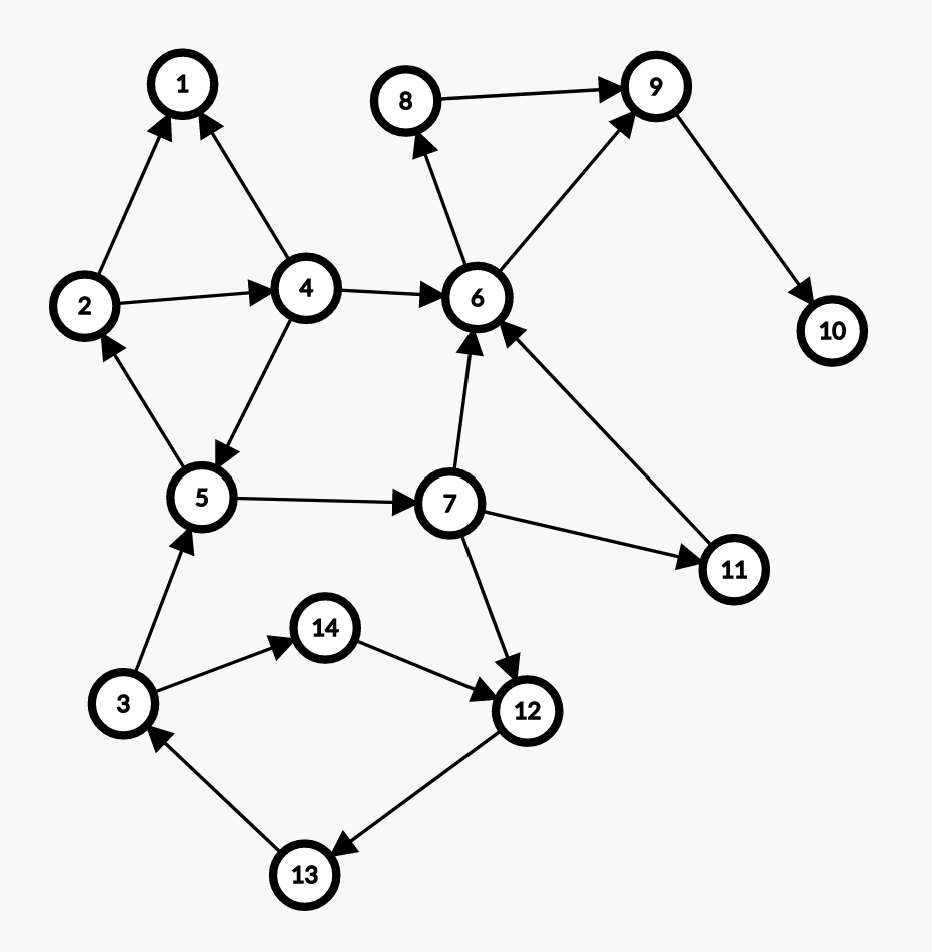
可以手动模拟一下上图，更好的理解代码，如不理解，请评论。

Tarjan 求 SCC 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 4;
struct node {
	int to, nx;
} eg[N];
int hd[N], tot;
void adeg(int st, int ed) {
	eg[++tot] = {ed, hd[st]};
	hd[st] = tot;
} //链式前向星
int dfn[N], low[N], tt, cnt;
//含义如上文所解释
bitset<N> instk; //记录节点是否在栈中
stack<int> stk; //dfs 栈
vector<int> scc[N]; //每个 SCC 中包含哪些节点
int bel[N]; //每个节点属于的 SCC 编号
void tarjan(int u) {
	dfn[u] = low[u] = ++tt;
	stk.push(u);
	instk[u] = 1;
	for (int i = hd[u]; i; i = eg[i].nx) {
		int to = eg[i].to;
		if (!dfn[to]) tarjan(to), low[u] = min(low[u], low[to]);
		//没搜索过的点，进行 dfs，并且更新 low[u]
		else if (instk[to]) low[u] = min(low[u], dfn[to]);
		//对于返祖边，更新 low[u]
	}
	if (dfn[u] == low[u]) {
		//如果该节点是强连通分量头，进行退栈操作
		++cnt;
		while (true) {
			int tp = stk.top();
			stk.pop();
			instk[tp] = 0;
			bel[tp] = cnt;
			scc[cnt].push_back(tp);
			//退栈同时记录墙连通分量
			if (tp == u) break;
			//如果 u 已退栈，那么结束退栈操作
		}
	}
}
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr),
	        cout.tie(nullptr);
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= m; ++i) {
		int u, v;
		cin >> u >> v;
		adeg(u, v);
	}
	for (int i = 1; i <= n; ++i)
		if (!dfn[i])
			tarjan(i);
	//对于每一个没有进行过计算的点，都跑一次 tarjan
	//否则有可能因为图不连通或者其他原因导致一些漏算
	cout << cnt << '\n';
	for (int i = 1; i <= cnt; ++i) {
		for (auto c : scc[i])
			cout << c << ' ';
		cout << '\n';
	} //输出强连通分量
	return 0;
}

通过 SCC 缩点后，可以整张图会变成一个 DAG，可以参考 DAG 上问题这篇文章求解最长路和拓扑序。