DAG 拓扑排序和最长路

DAG（有向无环图）

what is DAG?

DAG（Directed acyclic graph）中文名称是有向无环图，简单来说，就是对于一个无回路的有向图。

如果一个有向图无法从任一个顶点出发经过若干条边回到该点，则这个图是一个有向无环图（DAG）。

有向无环图和树的关系：

因为有向图中一个点经过两种路线到达另一个点未必形成环，因此有向无环图未必能转化成树，但任何有向树均为有向无环图。

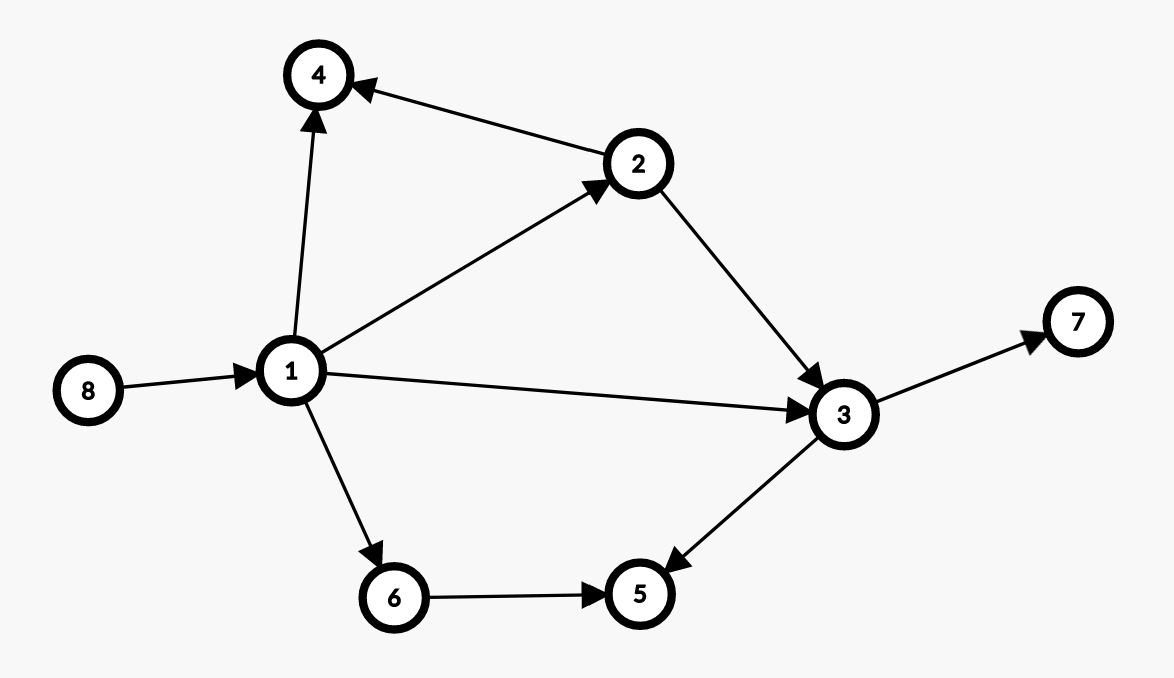
比如上图就是一个有向无环图，但是它不是树。

DAG 的性质与应用

性质

有向无环图一定存在拓扑序。
在一个有向无环图上，可以进行最长路的求解，具体做法为拓扑排序后进行 bfs。
在讲 kosaraju 时，我引用了一句话：“Every graph is the DAG of its strong connected conponents.”，译为“每个图都是关于其强连通分量的有向无环图”，那么，也就是说，我们按照强连通分量缩点，那么缩点后得到的新图一定是一个 DAG。

应用

有向无环图是描述含有公共子式的表达式的有效工具。
有向无环图是描述一项工程或系统的进行过程的有效工具。

拓扑排序

什么是拓扑序？

对一个有向无环图 $G$ 进行拓扑排序，是将 $G$ 中所有顶点排成一个线性序列，使得图中任意一对顶点 $u$ 和 $v$ ，若边 $<u,v>\in E(G)$ ，则 $u$ 在线性序列中出现在 $v$ 之前。通常，这样的线性序列称为满足拓扑次序（Topological Order）。

也就是说，对于书上每一条边，若其从 $u$ 连向 $v$ ， $ord(u)$ 表示节点 $u$ 的拓扑序， $ord(v)$ 表示节点 $u$ 的拓扑序，一定满足 $ord(u)<ord(v)$ 。

如何求解拓扑序？

在讲有向无环图的时候，提到“有向无环图有唯一的拓扑序”。

选择一个入度为 $0$ 的顶点并输出；
从网中删除此顶点及所有出边。

循环结束后，若输出的顶点数小于网中的顶点数，那么说明图中有环，否则输出的顶点序列就是一种拓扑序列。

拓扑排序代码

int in[N],ord[N],ct;
vector<pair<int,int> > vc;
void tp(int n) {
	queue<int> q;
	for(int i=1;i<=n;++i)
		for(int j=hd[i];j;j=eg[j].nx) {
			int to=eg[i].to;
			in[to]++;
		}
	for(int i=1;i<=n;++i) if(!in[i]) q.push(i);
	while(q.size()) {
		int tp=q.front();
		q.pop();
		ord[tp]=++ct;
		vc.push_back(make_pair(ct,tp));
		for(int i=hd[tp];i;i=eg[i].nx) {
			int to=eg[i].to;
			in[to]--;
			if(!in[to]) q.push(to);
		}
	} sort(vc.begin(),vc.end());
}

拓扑排序和 tarjan 或 kosaraju 结合，可以解决大量的图上难题。G 的前置知识点以及 DAG 的性质。

DAG 上最长路

对于一张普通图，若边权全部为正，那么我们不能求解其拓扑序，因为不论使用 Dijkstra 还是 SPFA，都会调入“正权回路”的深渊。

而在有向无环图上，无论边权正负，由于没有环，所以也没有回路，所以我们可以求最长路。

如何求解最长路

对于每个点跑单源最短路，由于是有向无环，所以任意两点间至多有 $1$ 条路经，对于每个节点，我们都从它出发，进行一次 bfs（有点像 floodfill），然后类似 SPFA 地，进行入队和松弛。

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e4+7, M = 2e5+7;
struct node{
	int to,nx;
} eg[M];
int hd[N],tot;
void adeg(int u,int v) {
	eg[++tot]={v,hd[u]};
	hd[u]=tot;
}
int dis[N],w[N];
void bfs(int i) {
	queue<int> q;
	dis[i]=wt[i];
	q.push(i);
	while(q.size()) {
		int tp=q.front();
		q.pop();
		for(int i=hd[tp];i;i=eg[i].nx) {
			int to=eg[i].to;
			if(dis[tp]+wt[to]>dis[to]) {
				dis[to]=dis[tp]+wt[to];
				q.push(to);
			}
		}
	}
}
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr),
	cout.tie(nullptr);
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;++i) cin>>w[i];
	for(int i=1,u,v;i<=m;++i) {
		cin>>u>>t;
		adeg(u,t);
	} int res=0;
	for(int i=1;i<=n;++i) bfs(i);
	for(int j=1;j<=n;++j) res=max(res,dis[j]);
	cout<<res<<'\n';
	return 0;
}

⭐️补充：源汇思想

在有一个联通的有向无环图中，会有两种点，第一种点叫做 source（中文译为源），另一种 sink（中文译为汇），源就好比江河的源头（只有出度没有入度的点），汇就好比江河所汇入的大海（只有入读没有出度的点）。

比如，下图中，节点 $1$ 和 $10$ 就是源，而节点 $2$ 、 $4$ 和 $9$ 都为汇：

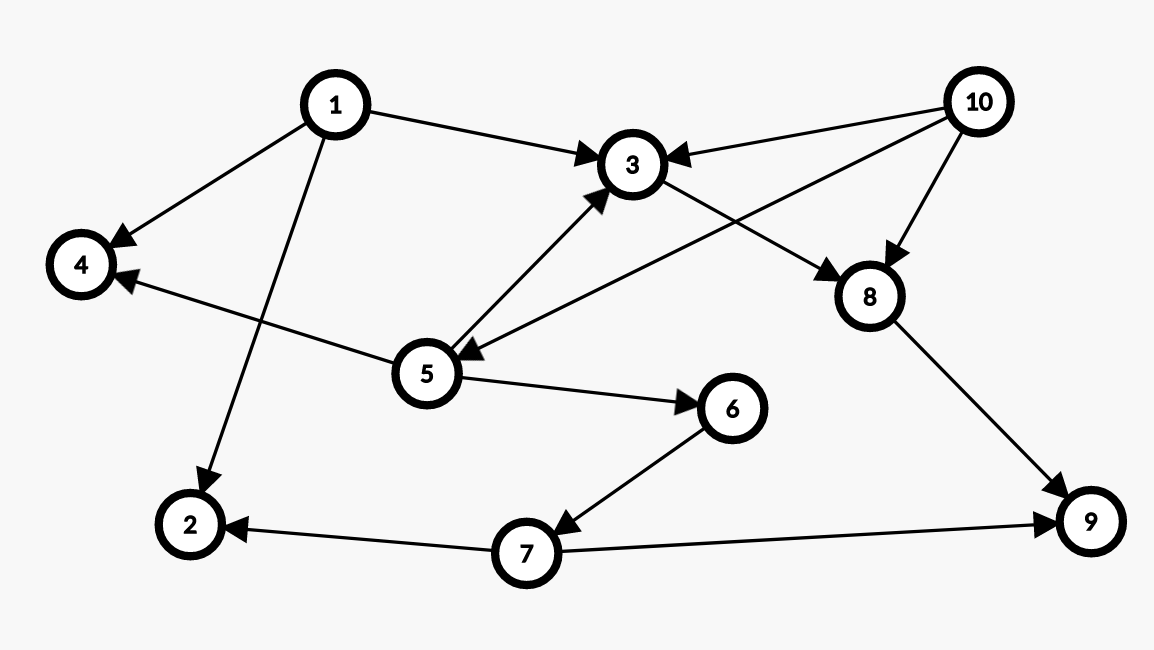
可以发现以下几点性质：

不是所有节点都要么是源、要么是汇；
对于有向无环图，至少有一个源和一个汇；
源的拓扑序永远在先，汇的拓扑序永远在后；
如果把一个原本弱联通的 DAG 的源和汇相连（从汇指向源），且保证每个源都连接至少一个汇，每个汇都至少有一个源与之相连，那么整个 DAG 就会变成一个强连通分量（也就是说，若想让一个 DAG 中任意两点都可以相互到达，那么需要加的边的数量是源和汇个数的最大值）。